עירובין נו ב
| ראשונים נוספים על הש"ס: ראשונים | אחרונים
תנו רבנן אהמרבע את העיר עושה אותה כמין טבלא מרובעת וחוזר ומרבע את התחומין ועושה אותן כמין טבלא מרובעת וכשהוא מודד לא ימדוד מאמצע הקרן אלפים אמה מפני שהוא מפסיד את הזויות אלא מביא טבלא מרובעת:
שהיא אלפים אמה על אלפים אמה ומניחה בקרן באלכסונה נמצאת העיר משתכרת ארבע מאות אמות לכאן וארבע מאות אמות לכאן נמצאו תחומין משתכרין ח' מאות אמות לכאן ושמונה מאות לכאן נמצאו העיר ותחומין משתכרין אלף ומאתים לכאן ואלף ומאתים לכאן אמר אביי ומשכחת לה במתא דהויא תרי אלפי אתרי אלפי תניא אמר רבי אליעזר ברבי יוסי בתחום ערי לוים אלפים אמה צא מהן אלף אמה מגרש נמצא מגרש רביע והשאר שדות וכרמים מנא הני מילי אמר רבא דאמר קרא (במדבר לה, ד) מקיר העיר וחוצה אלף אמה סביב אמרה תורה סבב את העיר באלף נמצא מגרש רביע רביע פלגא הוי אמר רבא בר אדא משוחאה אסברה לי משכחת לה במתא דהויא תרי אלפי אתרי אלפי תחום כמה הויא שיתסר קרנות כמה הויין שיתסר דל תמניא דתחומין וארבעה דקרנות כמה הוי תריסר נמצא מגרש רביע טפי מתלתא נינהו אייתי ארבעה דמתא שדי עלייהו אכתי תילתא הוי מי סברת בריבועא קאמר בעיגולא קאמר כמה מרובע יתר על העגול רביע דל רביע מינייהו פשו להו תשעה ותשעה מתלתין ושיתא ריבעא הוי אביי אמר משכחת לה נמי במתא דהויא אלפא באלפא תחומין כמה הוו תמניא קרנות כמה הוי. שיתסר
רש"י
[עריכה]
המרבע עיר - עגולה:
עושין לה כמין טבלא מרובעת - לקמן מוקי לה במתא דהויא תרי אלפי אתרי אלפי בעיגולא שכשאתה מוסיף ריבוע עליה הרי היא כמין טבלא מרובעת אורכה כרוחבה ותחומיה כמין טבלא מרובעת אורכן כרחבן רחבן למדת העיר על פני חומתה שהיא אלפים וכן אורכן להלן מן העיר אלפים והיינו דקאמר חוזר ומרבע את התחומין כלומר חוזר ומודד לה תחומיה ועל כרחך מרובעין הן:
וכשהוא מודד - תחומי העיר לאחר שריבעה לא ימדוד מאמצע קרן זוית של עיר כנגדו באלכסון אלפים לכל קרן וקרן למתוח חוט מתחום קרן זה לתחום קרן זה:
מפני שמפסיד את הזויות - לכל קרן וקרן מפסיד מה שאלכסון של אלפים על אלפים עודף על ריבוע וכשמותח החוט לא תמצא באורך התחומין מן העיר והלאה לכל צד אלא אלף ותכ"ח אמות כיצד תן תחומין של אלף ותכ"ח אורך לכל צד כנגד העיר אתה צריך לתת טבלא של אלף ותכ"ח על אלף ותכ"ח לכל קרן למלאות פגימתן של אורך בריבוע שיהו התחומין מרובעין שהרי ריבוע פיאות לכל שובתי שבת ותמצא באלכסונו של טבלא מכוון כנגד אלכסון קרן העיר אלפים דקיימא לן כל אמתא בריבוע אמתא ותרי חומשי באלכסונה טבלא של אלף ותכ"ח על אלף ותכ"ח אלכסון שלה עודף אלפים ותתנ"ו חומשין שהן תקע"ב אמה פחות ד' חומשין תנם על אלף ותכ"ח הרי אלפים נמצא כשמדדת מאמצע קרן העיר באלכסון אלפים קיצרת את התחום ואינן אלא אלף ותכ"ח וכל כך למה מפני שהפסדת את הזויות שהיית צריך למדוד אלפים ואלכסונן מאמצע קרן העיר ולמתוח חוט אחרי כן מתחום קרן לתחום קרן ותמצא מן החוט ולעיר על פני כל העיר לכל צד אלפים אמה כיצד תן אלפים תחום כנגד העיר לארבע רוחותיה תמצא פגימת אלפים על אלפים לכל קרן ועדיין אתה צריך למתוח חוט כמין גאם להשוות תחומי הקרנות לתחומי העיר ותמצא לכל קרן טבלא של אלפים על אלפים ומכוון אלכסונה כנגד אלכסון קרן העיר ומהו אלכסונה אלפים ות"ת אמה שכך עולה חשבון ד' אלפים חומשין לח' מאות אמה לפיכך הבא למדוד תחומי העיר מביא טבלא רואה כאילו הביא טבלא שהיא אלפים על אלפים ומניחה כנגד העיר באלכסון אלכסון של טבלא כנגד אלכסון של קרן כלומר מודד אלפים וח' מאות כנגד הקרן באלכסון ואח"כ מותח חוט מתחום קרן לתחום קרן:
נמצא העיר משתכרת - במה שרבענוה ד' מאות אמה לכל קרן וקרן שכשהיתה עגולה לא היה לה אלכסון ועכשיו שריבענוה נתננו לה אלכסון והיוצא דרך הקרן משתכר ת' אמה לקרן זו ות' אמה לקרן זו:
נמצאו תחומי הקרנות משתכרין - במה שנתננו טבלא באלכסון כנגד הקרן ח' מאות לכל קרן:
צא מהן - סביב העיר אלף אמה למגרש שאין נוטעין ולא זורעין שם אלא מניחין אותו לנוי העיר כדמתרגם רווחי קרויא:
נמצא מגרש רביעי - לקמן מפרש:
והשאר - שאר התחום שדות וכרמים וחוץ לתחום לא היה להן כלום:
מנא הני מילי - דמגרש אלף אמה:
מקיר העיר - רישא דקרא ומגרשי הערים אשר תתנו:
בר אדא - שם האיש:
משוחאה - מציין תחומי העיר:
תחומין כמה הוו שיתסר - י"ו רבעין של אלף על אלף יש בהן כיצד אלפים על אלפים לכל צד חלקם שתי וערב הרי ד' רבעין של אלף על אלף וכן לכל רוח של עיר:
קרנות כמה הוו - תחומי הקרנות של תחומין נמי שיתסר נינהו שהרי לכל קרן יש טבלא של אלפים על אלפים כדמפרשינן לעיל:
דל - לצורך מגרש:
ח' דתחומין וד' דקרנות - דהא אמרת סבב את העיר באלף הרי לכל התחום אלפים על פני העיר באורך וברוחב אלף להלן מן העיר וכיון שנתת אלף בליטת מגרש לד' רוחות צריך אתה ליתן לכל קרן טבלא של אלף על אלף הא ארבעה מן הקרנות למגרש הא תריסר לצורך מגרש כולן אלף על אלף:
נמצא מגרש רביע - בתמיה:
אייתי ארבעה דמתא שדי עלייהו - דתלתין ותרין והוו להו תלתין ושית דהא דקתני מגרש רביע אכולה מילתא קאי רביע החשבון כולו של עיר ותחומין וקרנות. כמה מרובע יותר על העגול רביע דל ריבעא מיניה כו'. את חשבת בעיר מרובעת ועבדת מגרש סביב נמי בריבוע לפיכך עלה חשבון העיר ומגרשיה ד' אלפים על ד' אלפים מרובעין שהן י"ו רבעין של אלף על אלף ומהן ג' חלקים למגרש והיינו תריסר וחלק הרביעי לעיר ואנן במתא עגולתא עסקינן כדמוקמינן לקמן ומכל מקום אנו מוסיפין עליה לתת ללויים ריבועא עמה וקרנותיה ותחומין אלפים לכל רוח הרי חלק הלויים סך הכל ששת אלפים שהן תלתין ושית רבעין של אלף על אלף והעיר באמצעיתן עגולה אלפים ומגרשיה סביב לה אלף רוחב נמצאת עיר ומגרשיה ד' אלפים על ד' אלפים עגולין ואם היו ד' על ד' מרובעין הוו שיתסר השתא דעגולין דל ריבעא הוו תריסר ומהן ג' חלקים למגרש והרביעי לעיר דהוו להו ט' מגרשין וט' מתלתין ושית הניתנין ללויים ריבעא הוו:
משכחת לה נמי במתא דהויא אלפא אאלפא - ולא תחשוב העיר אליהן אלא נמצא מגרש רביע אתחומין וקרנות קאי:
תחומין כמה הוו תמניא - רבעין של אלף על אלף שהרי תחום לכל צד אלפים אורך להלן מן העיר ואלף רוחב על פני העיר וקרנות שיתסר דכיון דאורך התחומין משוכין אלפים לכל צד אתה צריך למלאות פגם לכל קרן בטבלא אלפים על אלפים:
תוספות
[עריכה]
פלגא הוי. פירוש מגרש דתחומין הוי פלגא דתחומין ולא רצה לדקדק ולהקשות דמגרש דתחומין והקרנות כך וכך הוי מתחומין וקרנות משום דפעמים הוי תלתא או רביע או חומש מן התחומין ומן הקרנות לפי מה שהעיר גדולה או קטנה:
משכחת לה במתא. הקשה השר מקוצי דמשכחת לה מגרש רביע דתחומין וקרנות במתא דהוי ח' אלפים על ח' אלפים ומגרש הוי ל"ו ותחומין וקרנות ומתא הוו קמ"ד פעמים אלף על אלף וי"ל דערי מקלט אינן גדולים כל כך כדאמר בפרק אלו הן הגולין (מכות דף י.) ערים הללו אין עושין אותם לא גדולות ולא קטנות ומהר"י אומר שמתרץ האמת דהשתא קמ"ל דמגרש אינו מרובע כדמסיק ולרבינא קמ"ל דאין מגרש לקרנות ולרב אשי דאין מגרש אלא לקרנות אבל בכה"ג לא היה משמיענו שום חידוש:
כמה מרובע יתר על העגול רביע. ואור"י דהא רביע בין בהיקף בין בגוף הקרקע כדאמר הכא נמצא מגרש רביע וכן משמע גבי ים שעשה שלמה (לעיל דף יד:) ועל ההיקף יש להוכיח בהדיא כדפ"ה דכל שברחבו טפח יש בהיקפו ג' טפחים ובטפח מרובע יש בהיקפו ד' טפחים ועל הקרקע שבפנים יש להוכיח נמי שאם תקיף טפח עגול סביב בחוטין דקין עד הנקודה האמצעי' שבעגול ותחתוך מן הנקודה ולמטה כל החוטין לב' ותפשטם יהיה העליון ארוך ג' טפחים והאחרים מתקצרים והולכים עד הנקודה שהוא חצי טפח מן החוט העליון תחתוך שוב כל החוטין לשנים ושים הארוך בצד הקצר נמצא הרבוע אורכו טפח וחצי ורחבו חצי טפח דהיינו שלש חתיכות של חצי טפח על חצי טפח ובטפח מרובע יש ד' חלקים של חצי טפח על חצי טפח:
אביי אמר משכחת. ואם תאמר לפי מה דמוקי לה לקמן במתא עגולה קשה דתחומין הוו טפי כמו שאנו מרבעין העיר ולא הוי מגרש רביע מהם ויש לומר דלא קאמר מגרש רביע אלא מתחומין שבחוץ לריבוע העיר:
עין משפט ונר מצוה
[עריכה]מתוך: עין משפט ונר מצוה/עירובין/פרק ה (עריכה)
כב א מיי' פכ"ח מהל' שבת הלכה ו' והלכה ז, סמ"ג לאוין סו, טור ושו"ע או"ח סי' שצ"ט סעיף י':
כג ב מיי' פי"ג מהל' שמיטה ויובל הלכה ב', סמג עשין קכה:
ראשונים נוספים
ושנה אחרת ואט"ד [סי' ועי' ברש"י]. אמר שמואל אין בין תקופה לתקופה אלא ז' שעות ומחצה ואין תקופה מושכת מחברתה אלא חצי שעה. אלו כולן פשוטות הן. ואמר שמואל אין לך תקופת ניסן שנופלת בצדק שאינה משברת את האילנות ואין תקופת טבת נופלת בצדק שמייבשת האילנו' והוא דאתייליד לבנה או בלבנה או בצדק:
ת"ר המרבע את העיר עושה אותה כמין טבלא מרובעת המרבע תחומין עושין אותן כמין טבלא מרובעת.
כשהוא מודד לא ימדוד מאמצע הקרן מפני שמפסיד הזויות אלא מביא טבלא שהיא אלפים על אלפים ומניחה כנגד הקרן באלכסון נמצאת העיר משתכרת הזויות. ת' אמה לכאן ות' אמה לכאן נמצאו תחומין משתכרין ת"ת אמה לכאן ות"ת אמה לכאן נמצאת העיר ותחומיה משתכרין אלף ומאתים אמה לכאן ואלף ומאתים אמה לכאן.
אמר אביי משכחת לה במאתא דהיא אלפים אמה על אלפים אמה. פי' זו העיר שהעמדנוה אלפים על אלפים עגולה היא וכבר אמרנו למעלה שצריך למדידת תחומין פיאות לפיכך צריכין להוסיף על אלפים אמה הללו העודף המרובע על העיגול והוא כדמסיקנא לה בסיפא דשמעתא דאמרינן הכי כל אמתא בריבוע אמתא ותרין חומשי באלכסונא הלכך נמצא באלפים על אלפים עודף ד' אלפים חומשין שהוא ת"ת אמה. נמצא עודף בעיר שהיא אלפים על אלפים ת"ת אמה. ובמזרח בתחומין שהן אלפים על אלפים ת"ת אחרונות וכן במערב נמצא העודף אלפים אמה ות' אמה כשתחלקם נמצא חציים אלף ומאתים אמה תופסת על אלפים לתחום המזרח ואלף ומאתים לתחום המערב נמצא התחום חוץ לעיר ג' אלפים ומאתים אמה.
תניא ר' אליעזר בנו של ריה"ג אמר תחום ערי לוים אלפים. צא מהן אלף אמה מגרש והשאר לשדות וכרמים. נמצא מגרש רביע. ואקשינן מכדי תחום כמה הוי אלפים כשתוציא ותסבב העיר באלף נשארו אלף אחרות הנה החצי איך שנה מגרש רביע אלפים אמה אורך ברוחב אלף וכן בצפון וכן במערב וכן בדרום. נמצאו בד' צדדי העיר ט"ז אלף אורך ברוחב אלף וצריך למלאות הקרנות אלפים אורך ברוחב אלפים על כל זוית וזוית נמצאו ד' קרנות עוד ט"ז אלף אמה באורך ורוחב אלף אמה ושיעור המגרש סביבות העיר אלף רוחב. וכיון שהעיר היא אלפים על אלפים נמצאו בד' צדדי העיר אלפים אמה אורך ברוחב אלף שמונת אלפים אורך ברוחב אלף. גם יש לה למלאות הקרנות בד' זויותיה אלף על אלף בכל זוית שהן ד' אלפים אמה נמצא מגרש בסבוב העיר כולה עם הקרנות י"ב אלף אמה. ותחום העיר וקרנותיה הויין (י"ב ש"ב) [ל"ב אלפים] אמה הנה י"ב אלף שהן מגרש לגבי ל"ב של תחומין טפי מתלתא הויין ופרקינן אייתי ארבע דמתא. כלומר תוך העיר אלפים על אלפים עושין ד' אלפים אורך ברוחב אלף אמה הוסיף אותם בכלל ל"ב אמה נמצאו הכל [ששה ושלשים] אלפים אמה ואכתי י"ב אלף מששה ושלשים אלף שליש הן איך שנינו נמצא מגרש רביע.
ופרקינן מי סברת האי מגרש בריבועא הוא בעיגולא הוא פחות שליש. ואיכא למימר מתא נמי עיגולא היא והכי קאמר רחמנא מקיר העיר וחוצה וגו' צריך סביבות העיר כולה אלף אמה ולגבי תחומין יהבינן לה פאות כר' חנינא דתני זה יהיה לכם כזה יהיו כל שובתי שבת. אבל לגבי מגרש לא יהבינן ליה פיאות הלכך הסר מהן יתרון שמעדף המרובע על העיגול וכמה הוא היתרון רביע נמצא רביע י"ב אלף ג' אלפים כשתפחות מי"ב אלף ג' אלפים נמצא המגרש ט' אלפים אמה. והתחומין עם העיר והקרנות הן ל"ו אלף אמה נמצאות ט' אלפים אמה מל"ו אלף רביע שלהן וזוהי ששנינו נמצא מגרש רביע.
וכשהוא מודד לא ימדוד מאמצע הקרן מפני שהוא מפסיד את הזויות: פירש רש"י ז"ל: לא ימדוד כנגד הקרנות אלפים באלכסון לכל קרן וקרן, שא"כ כשהוא מותח חוט מתחום קרן זה לתחום קרן זה, נמצא שהוא מקצר את התחומין הרבה עד שלא תמצא באורך התחומין מן העיר והלאה לאורך התחומין כי אם אלף תכ"ח אמות ויותר משהו, כי מרובע (מאלכסונו) שאלכסונו אלפים אינו אלא אלף ותכ"ח על אלף ותכ"ח ויותר משהו. ואינו מחוור בעיני שאם כן לא היה לו לתנא דברייתא לומר כן שהוא מפסיד את הזויות שהרי אין זה מפסיד בזויות דהא יש לו בזויות אלפים אמה אלא בתחומין הוא מפסיד, ואם מפני שההפסד בא לו מצד הזויות, היה לו לומר מפני שהוא מפסיד מפני הזויות.
נמצא מגרש רביע, פלגא הוי: כלומר: אם התנא חושב תחום מגרש בלא קרנות כנגד תחומי העיר בלא קרנות ואפילו יחשוב מגרש וקרנותיו עם תחומין וקרנותיהן, אכתי לא הוי רביע, אלא משום דשיעורא לא פסיקא ליה כי מעילת קרנות בחשובנא ושניא שיעורא בין עיר גדולה לקטנה, משום הכי לא חש לעיולי השתא קרנות בקושיא, כיון דסוף סוף אפילו כי מעילת להו לא הוי. וכן כתב הראב"ד ז"ל. ומסתברא לי משום דאכתי לא פסיקא ליה אי יהבינן קרנות למגרש אם לאו, דדילמא מאי סביב דתחומין ולא דקרנות, וכדסבירא ליה נמי לרבינא בסמוך, ותנא לא חשיב תחום מגרש אלא כנגד תחום העיר ולא כנגד תחום העיר והקרנות, כיון שאין למגרש קרנות, ורביע מינה קאמר. ומיהו דכשתמצא לומר דיש לו קרנות למגרש אכתי לא הוי.
מי סברת בריבוע קאמרינן בעיגולא קאמרינן: ובמתא עגילתא כדאמרינן במסקנא כמה מרובע יתר על העיגול רביע דל רביע מינייהו פש להו תשעה. ואע"ג דכי מפקא מן קרתא רביע והויא לה עגילתא עגול שוה כמין טבעת אלפים חוט ששה מקיף אותה, על דרך מה שאמרו (לעיל יג, ב) כל שיש ברחבו טפח יש בהקפו שלשה טפחים. הני מילי בחוט שהחוט הסובב את העיר ממש די לו בששה, אבל כיון שתחומי המגרש רחבן אלף, נמצא שאתה מוסיף למזרח העיר אלף ולמערב כנגדו אלף, וכן לצפון וכן לדרום, ונמצא עיר ומגרשיה ארבעת אלפים על ארבעת אלפים עגולין, וחוט חיצון המקיף אותן הוי י"ב אלפים. ולפיכך כיון שהחוט הפנימי של חודו של מגרש הסמוך לעיר הוי ששה, וחוט חודו החיצון של מגרש הוי י"ב, כשתתן ששה על י"ב הוי י"ח, וכשתשוה את הכל להיות טבלא אחת שוה עליונה כתחתונה, יצא לך טבלא של תשעה.
אביי אמר משכחת לה נמי במתא דהויא אלפא באלפא: אביי בא עכשיו להעמידה בתחומין לבד בלא שתכניס חשבון העיר בכלל. ומ"מ לא משכחת לה אלא במתא עגילתא, והיינו דאקשיתה אכתי לרבינא, ומשום הכי אוקמה בעיר מרובעת, ומאי רביע רביע דתחומין. כלומר: תחומי מגרש הוו רביע כל התחומין, לומר שהמגרש אין לו אלא תחומין אבל לא הקרנות, כי כל הקרנות נחשבין כתחומי העיר לשדות וכרמים, והלכך הוו תחומי מגרש רביע הכל. ומיהו לא משכחת לה אלא בעיר של אלפים על אלפים, ועל כן בא רב אשי וחידש דתנא מילתא פסיקתא קאמר, ובכל עיר בין בעגולה בין במרובעת בין גדולה בין קטנה, לפי שהמגרש אינו אלא בקרנות לבד כדמפרש ואזיל, וקרנות כולן שיתסרי אלפין הוי, דל ארבעה למגרש אלף לכל קרן, ארבעה לפום שיתסר ריבעא הוי.
ת"ר המרבע את העיר עוש' כטבלא מרובעת: פי' מרובעת ממש מכל צד ומוקים לה לקמן כשהיתה תרי אלפי על תרי אלפי כשהית' עגולה עכשיו כשמרבע' עושה אות' מרובעת מאלפים על אלפים ג"כ:
והמרבע את התחומין פי' כי אחר שירבע את העיר ויתן להתחומין מכל צד אלפים אמה עושה אות' ג"כ לכל צד כמין טבלא מרובעת שהרי אורך כל רוח ורוח מן העיר אלפים אמה והוא נותן לכל רוח אלפים אמה ונותן לכל קרן וקרן ג"כ כדי לרבעה טבלא של אלפים אמה על אלפים אמה נמצא העיר ותחומיה בטבלא מרובעת ששת אלפים על ששת אלפים שהרי היא היתה בתחלה אלפים ונתן למזרח אלפים וכן למערב הרי ששת אלפים ממזרח במערב וכן אתה אומר לצפון ולדרום. וכשהוא מודד לא ימדוד מאמצע הקרן מפני שהוא מפסיד את הזויות פי' רש"י ז"ל כשהוא מודד את התחומין לתת אלפים אמה לכל רוח. לא ימדוד מאמצע הקרן לתת אלפים אמה כנגד קרן וקרן באלכסון שא"כ הוא מפחית ומפסיד את הזוייות התם כי מפחית מאלכסונם והוא גורם ג"כ לפחות תחומי הצדדין כי כשיהא אלכסון הקרן אלפים אמה ויתן חוט מקרן שממזרחית דרומית לקרן מערבית דרומית לא יהיו התחומין שבצדדין אלא אלף תכ"ח ויותר משהו לפי הכלל שבידנו דכל אמתא ברבוע אמתא ותרי חומשי באלכסונה כי האלף עולין אלף ת"י ואתם עולין תק"ס והכ"ח עולין ל"ו חומשין שהם י"א אמה וחומש נמצא הכל אלפים אמה פחות מד' חומשין. נמצאת למד כיון שאין באלכסונו של הקרן אלא אלפים אמה שאין בלוח הרבוע אלא אלף תכ"ח ואלו היה מרבע התחומין כראוי היה נותן לכל רוח אלפים אמה שלמים ויהא באלכסונו של קרן אלפים ת"ת אמות נמצא מפסיד עכשיו לכל קרן ת"ת אמות לכל רוח מארבע רוחות העיר תקנ"ב אמו' סביבות העיר:
והא דקאמר מפני שמפסיד את הזויות: פרש"י ז"ל ששמפחית מדתם. וה"ה שמפחית מדת התחומין אלא דנקט חדא מינייהו ונקט את הזויות שהם הגורמים תחומי הפסד תחומי הצדדין. ואין לשון הש"ס מתיישב לפי שטה זו ועוד דלאו בשופטני עסקינן שלא יתן בתחומי העיר מן הצד כי אם אלף תכ"ח שהרי הדבר ידוע ושגור בפי הכל שיש לו למדוד אלפים אמה לכל רוח והפי' הנכון כך הוא כי אחר שימדוד אלפים אמה לכל רוח ויש למדוד כנגד הקרנות לא ימדוד שם אלפים אמה בלבד שא"כ הרי הוא מפסיד את הזויות כשיעור האלכסון דהיינו ת"ת אמות כי מרובע של אלפים על אלפים יש באלכסונו אלפים ושמנה מדות. וזו היא צורתה 
אלא כיצד הוא עושה אחר שימדוד לכל רוח ורוח סביבות העיר אלפים מבלי הקרנות מביא טבלא שהיא אלפים על אלפים ומניחם כנגד הקרן באלכסון כגון זה 
נמצאת עיר משתכר' ד' אמות אמ' לכאן וד' אמות אמה לכאן פיי' כי כשהיתה העגולה ועשאוה מרובעת עלה האלכסון שלה לאלפים ת"ת ונשתכרה בכל קרן וקרן ד' מאות. ונמצאו תחומין משתכרין שמונ' מאו' לכאן ושמונה מאות לכאן פי' ת"ת אמות לכל קרן לפי שבכל יש אלפים על אלפיים מרובע' ועולה האלכסון לאלפים ת"ת. נמצא העיר ותחומה משתכרין אלף ומאתים אמה לכאן. פי' אלף ומאתים אמות לכל קרן ד' מאות לקרן העיר ות"ת לקרן התחום:
אמר אביי ומשכח' לה וכו' פי' משכח' לה להאי מתנית' במת' עגולת' דהוי' תרי אלפי על תרי אלפי וכמו שציירנו:
שם תניא ר"א בן יעקב אומר תחום ערי לוים אלפים צא מהם אלף אמה מגרש נמצ' מגרש רביע והשאר לשדות וכרמי' פי' דמגרש אלף אמה לכל רוח.
אמר רבא דאמר קרא וכו' ואקשי'. והיכי קתני נמצא מגרש רביע דהא פלגא הוי פי' פלגא דתחומין לכל רוח מלבד הקרנות דאלו בקרנות אכתי לא ידעי' כמה הוי והיכי הוי דאפשר דאין נותנין מגרש בקרנות כלל דדילמא מאי סביב סביב דתחומין בלבד וכדסבר רבינא לקמן ולא ידעי' נמי אם יהיו תחומי הקרנות מרובעת אשי לאו הילכך אע"פ שאם תחומי הקרנות מרובעת יעלה האלכסון לאלפים ת"ת ואין המגרש נוטל מהם אלא אלף אמה לא יהא המגרש פלגא בקרנות לא חיישי' להכי דסוף סוף לא הוי מגרש רביע וכיון דאכתי לא ידעי' דינא דקרנות לא חששנו להם ופרכי' מן התחומין דמגרש פלגא הוי ומהדרי' אמר רבה בר אדא משותאה אסברה לי דהא מתנייתא מיירי במתא דהוי' גופה תרי אלפי על תרי אלפי ופרכי' תחומין כמה הוו שיתא עשר חתיכו' שיש בכל חתיכה אלף על אלף שהרי התחומין לכל צד אלפים על אלפים שהם ד' חתיכות מרובעת מאלף על אלף נמצאת לד' רוחות שיתא עשר חתיכות קרנות כמה הוו שיתא עשר. פי' שהרי ד' קרנות הם וכשתרבע אותם לתת בכל טבלא קרן מרובעת יהיו ג"כ אלפי' על אלפי' בכל קרן. ויש בכל קרן ד' חתיכות מרובע' מאלף על אלף. הוו להו תחומין וקרנו' ל"ב חתיכו' דלתמניא דתחומין וד' קרנות אלף לכל קרן כגון זה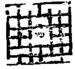 
וא"כ היכי קתני נמצא מגרש רביע דהא טפי מתלתא הוי כי חלק המגרש הוא י"ב אלפים מרובעין דאינון תלתא דל"ו אלפי' ואלו הכא ליכא בתחומין וקרנות אלא ל"ב. ומהדרינן אתי ד' דמת' שדי' עלייהו. פי' צריך אתה לכלל עם החתיכו' של תחומין וקרנות ד' חתיכות שיש בעיר מאלף על אלף והוו להו כלהו נ"ו חתיכות. ופרכי' דאכת יקשיא דהא מגרש תלתא דמתא ותחומין הוא דהוי והיכי קתני שהוא רביע ומהדרי' כמה מרובע יותר על העגול רביע דל ריבעא מנהון פשו להו תשעה תשעה לפום תלתין ושיתא רביע הוי. וה"פ כי באמת זו העיר שהיתה עגולה בתחלתה מב' אנפי על תרי אלפי רבענו אותם וגם רבענו תחומיה אלפים אמה לכל רוח מרובעת. עד שעלה סך חלקי' לתלתין ושיתא חתיכות של אלף על אלף ועשינו כל זה כדי להרבות בתחומי הלוים. אבל כשחוזרין לתת למגרש חלקו אלף אמה לכל רוח סביב אין נותנין כפי הרבוע הזה אלא כפי מה שהיה נופל לו סביבות העיר בעגול כשהיתה העיר עגולה וכל הרוח הנשאר מהאלפים אמה שיש לתחומין לכל רוח ברבוע הוא לשדות וכרמי'. וא"כ מאותן י"ב אלפים חתיכות שנפל למגרש מן התחומין ומן הקרנות כשהיתה העיר והתחומין מרובעין יש לנו לחסר מהם הרביע שיש במרובע יותר על העגול כי בתחלה היו העיר והמגרש ברבוע ששה עשר חתיכות ד' חתיכות לעיר וי"ב למגרש יש למגרש ג' חלקים ולעיר חלק אחד ועכשיו כשהחזרנו אות' לעיגול חזרו העיר והמגרש פחו' רביע והוו להו י"ב חתיכות חזרו הי"ב חתיכו' של מגרש ל"ט חתיכו' וחזרו ד' של עיר לג' חתיכות נמצא כי חלק המגרש שהוא ט' חתיכו' רבוע כל העיר וכל התחומין והקרע' שהם ל"ו חתיכות. זו שיטת התלמוד. ויש בו מקום עיון שהרי המגרש הזה כשהיה מרובע והיו בו י"ב חתיכות לא היה כלו מלא באמצע כעין טבלא מרובעות שהרי העיר היה בתוכה והמגרש היה היקף אחד מרובע ותוכו חלל רחב כל לוח ולוח אלף וארך כל רוחותיו סביב עם זויותיו י"ב אלפים. וא"כ כשחזרנו לעגל את העיר והמגרש היאך חסר רביע שלא אמרו מרובע יותר על העיגול רביע אלא בעיגול גמור כעין לבנה עגולה שכל תוכו מלוי מן המנין כי הזויות שנעשין סביבו' העיגול לכל ד' זויות עודפין על שטח העיגול שבתוכו רביע אבל בכאן היאך אפשר לומר כן וי"ל דאנן לאו מגרש באנפי נפשיה מרבעינן ומעגלינן אלא עיר ומגרש ביחד כאלו הכל גוף אחד מד' אלפים על ד' אלפים כי העיר היתה אלפים על אלפים וכשנתנו לכל רוח אלף מגרש היו ד' אלפים על ד' אלפים וכיון שהיה הכל גוף אחד מרובע היה המגרש ג' חלקים והרביע לעיר אף עכשיו כשנעשה הכל גוף אחד עגול טפל לו מן הנשאר שלשה חלקים ורביע לעיר ונמצא חלקו ט' אלפי' כמו שאמרנו וא"ת והלא המגרש הזה העגול שהו' כעין טבעת המקיף את העיר בעיגול יש בחוט הפנימי שלו הסמוך לעיר ששת אלפים ובחוט החיצון הסובב י"ב אלפים כיצד העיר היא עגולה תרי אלפי על תרי אלפי וכל עגול שיש ברחבו טפח יש בהקפו ג' נמצא שמקיף את העיר חוט א' של ששת אלפים. וכשנתת המגרש של אלף אמה סביב בעיגול היה כל העיגול ממגרש ועיר ארבעת אלפים על ד' אלפים שהרי נתת אלף אמה לכל קרן וכיון שרחב של עגול ד' אלפים החוט הסובב אותו מחוץ הוא י"ב אלפים נמצא טבעת המגרש חוט הפנימי ששת אלפים וחוט החיצון שני' עשר אלפים והיאך חזרו להיות ט' אלפים מרובעות. וי"ל כי כל טבעת עגול' כיוצ' בזה יש לך לערב מנין החוט החיצון עם מנין החוט הפנימי וניטול מחצי' הכל ויהי' בו מחצי' כל המנין מרוב' הילכ' טול י"ב שמבחוץ ותן אותו על ששה שבחוט הפנימי והוו להו י"ח מחציתם ט' מרובעות כי מה שחסר מן המנין למטה בחוט נשלם בעודף מלמעלה וכן אמרו המתעסקים בחכמת התשבורת:
אביי אמר משכחת לה נמי במתא דהוי אלפא על אלפא: פי' מעיר שהיתה עגולה מאלף על אלף נרבענו אותה ונתנו לה אלפים לכל רוח וקרן של אלפים על אלפים לכל זויות וזיות ורביע דקתני היינו שיש במגרש רביע התחומין והקרנות בלבד ולא הכניס בו חשבון העיר. ופרכינן תחומין כמה הוה תמניא אלפין לד' רוחות שהרי יש לכל רוח שני אלפים ארך באלף אמה רחב וקרנו' כמה הוו שיתא עשר פי' שהרי אף בזה יש אלפים על אלפים אמה לכל קרן ויש ארבעת אלפים מרובע' לכל קרן והוו שיתא עשר נמצא בין תחומין וקרנו' כ"ד חתיכו' מרובע' מאלף עד אלף דלארבע דתחומין וד' קרנות פי' טול חלק המגרש שהוא מחצי' התחומין דהיינו ד' חתיכות. וד' חתיכו' מן הקרנו' חתיכה אח' מכל קרן הוו להו תמניא וא"כ תלתא הוי והיכי קתני רביע ומהדרי' כמה מרובע יותר על העיגול רביע דלרבעא מינייהו פשו להו שיתא לפום עשרים וד' רבעא הוי פירושו כמו שפירשנו למעלה בדברי רבא כי אין לנו לחשוב במגרש אלא הנופל לו בעגול כלומר כשהעיר עגולה והמגרש עגול וכל השאר שהרוחנו בתחומין כשרבענו לעיר ולתחומיה הוא לשדו' וכרמים. מעתה העיר הזאת היתה עגולה אלף על אלף וכשאתה נותן סביבותיה אלף למגרש יהיה בעיגול זה שלשת אלפים על שלשת אלפים שהרי הוספנו עליו אלף לכל צד וקי"ל דכל שיש לעיגול ברחבו טפח יש בהקפו ג' טפחים א"כ ה"ל הקפו החיצון ט' אלפים והקפו הפנימי של חוט המגרש הסובב אל האלף הוא שלשת אלפים כשתערב מנין החוט החיצון עם מנין החוט הפנימי יהיו י"ב אלף וכשתשווה את הכל להיו' כטבלא מרובע' ותתן העודף מן החוט החיצון עם החוט הפנימי יעלה לך טבלא מרובע' מחצי הכל דהיינו ששת אלפים דה"ל רבעא דעשרי' וארבעה. ועל הדרך הזה. בעצמו יוצ' החשבון בדרך אחר כשתרבע את העיר ואת המגרש ותחזו' ותסלק מהם הרבוע ותחזיר' עגולי' כי בתחלה היתה עיר עגולה והרי רבענו אותה על אלף כשתתן אלף למגרש ברבוע סביב יהיו ג' אלפי' על ג' אלפי' מרובעי' שהם ט' אלפי' מפני סקרנו' נמצא העיר אלף על אלף והמגרש שמנת אלפים וכשתרצה לחשוב עגולי' תסיר מהם הרבוע כי המרובע יותר על העיגול רביע ומן הח' אלפים של המגרש דל מנייהו רביעא פשו להו ששת אלפים דהוי רבעא לפום עשרי' וארבעה. וזהו הדרך שתופס התלמוד בכאן לפי שטתו וכדברירנא כי מפני שכבר רבע כל העיר ותחומים להרווחת תחומי שדו' וכרמי' כשבא עכשיו לחשוב מה שנופל למגרש כפי מה שהיתה העיר עגולה והמגרש עגול מחשב אותו לפי חשבון מה שהמרובע יותר על העיגול ואינו מחשב אותו כפי מה שהיה כשהיתה העיר עגולה בתחלת' לחשבון כל שיש ברחבו טפח יש באלכסונו ג' טפחי' אבל הכא יוצא לחשבון אחר:
מתוך: מאירי על הש"ס/עירובין/פרק ה (עריכה)
עיר עגולה שכתבנו שמרבעין אותה צריך שתדע שאחר שרבעה צריך לעשותה כמן טבלא מרובעת ר"ל שיהא חוזר ומרבע את התחומין שאם לא כן הרי נשארו לו פגימות בכל הקרנות כשיעור הרבוע וזה שאמר וחוזר ומרבע את התחומין הוא פי' מה שאמר עושה אותה כמין טבלא מרובעת כלומר שאם לא ירבע את התחומין לא נמצאת העיר ברבועיה. כלה כטבלא מרובעת שהרי יש לה פגימה בכל קרן וקרן כשיעור רבוע שבצדו ונמצאו רבועיה כבליטות לה. וכשהוא מודד לרבע את התחומין לא ימדוד אלפים מאמצע קרן העיר באלכסון ר"ל מן הנקודה שבאמצע הקרן שממנה התחומין מתפצלין זה למזרח וזה לדרום וכן בשאר הרוחות שאם כן לא יהא רבועו של תשלום הפגם אלא אלף ותכ"ח אלכסונו מתרבה אלפים ותתנ"ו חומשין שהן תקע"ב אמות פחות ד' חומשין וכשתתנם על אלף ותכ"ח הרי אלפים ואחר שהוצרכת לרבעה הרי הוצרכת לעשות כל רבועי התחומין כתבניתו של קרן ונמצא שלא רבית ברבוע אלא אלף ותכ"ח ויתר משהו לתשלום הארבע חומשין כך פרשוה גדולי הרבנים. וגדולי הדור מקשים עליהם לענין פי' שלא היה לו לומר שמפסיד את הזוויות שהרי יש לו אלפים בזויות ובתחומין הוא שמפסיד ואם תאמר שקצורו בא לו מחמת (מניות) [מדידת] הזוית היה לו לומ' שמפסיד מחמת הזווית אלא שאפי' הוסיף ברבועיו אלפים ברבוע לכל צד כשרבע את העיר לא יאמר אף כשארבע את התחומין אין לי אלא אלפים לכל צד ואפי' בקרנות שהרי מפסיד בטבלאות של זויות שאין שם רבוע אלא אלף ותכ"ח ויתר משהו אלא מודד אלכסונות אלפים וארבע מאות שהוא רבוע אלפים. ונמצא לענין שכתבנו שבעיר שהוא אלפים על אלפים אתה משתכר תחלה ברבוע העיר לידון כגוף העיר ת' אמה בכל קרן והם ת"ת אמה לכאן באלכסון שמקרן מזרחי צפוני לקרן מערבי דרומי וברבוע התחומין שהוספת ארבע טבלאות של אלפים אתה משתכר ת"ת אמות באלכסונות טבלא זו וכשהוצאת קו באלכסון (עקרן) [מקרן] מזרחי דרומי של טבלא שהוספת בקרן זה לקרן מערבי צפוני של עצמה נמצאת ממשיך התחום בקו זה ח' מאות אמה לאותה טבלא וכן בקו אחד שתוציא בדרך זה מקרן מזרחי צפוני לקרן מערבי דרומי ונמצא שבעיר כזו ר"ל שהיא עגולה על צד שאחר הרבוע נעשית אלפים על אלפים שמשתכרת בין העיר והתחומין אלף ומאתים לכל קרן ארבע אמות של רבוע העיר לאותו קרן וח' אמות לאלכסון הטבלא שבאותו קרן בקרן מזרחי דרומי וכן הענין בקרן שכנגד אלכסונו במערב דרומי ונמצא בכל קרן ריוח אלף ומאתים בין אלכסון רבוע העיר ואלכסון הטבלא וכן בכל קרן ואלו מדדת מאמצע הקרן לא היה מגיעך מן הריוח בטבלא זו ריוח כל האלכסון אלא מקצתו. ועל דרך זה אתה מונה בעיר גדולה יתר מאלפים על אלפים שאתה משתכר ברבוע של עצמה לפי מה שהיא אבל בטבלאות של קרנות אי אתה מוסיף בהם ריוח לגודל העיר אלא הוצרך לאמר בה ומשכחת לה במתא דתרי אלפי' וכו' אלא לשכר רבוע של עצמה שהיא לפי מה שהיא העיר וזו היא צורתה# הרי אתה רואה בצורה זו שיש לה ארבע פגימות בארבע קרנות וכל פגימה מהן אלו אתה רוצה להשלימה בחוט יוצא כמין גאם מקרן רצועה עליונה לקרן רצועת הימין אתה צריך בה לטבלת אלפים על אלפים כשיעור הרבוע ואלו היית מודד בתשלומיהן אלפים אמה מאמצע קרן של רבוע העיר לא היה רבועה אלא אלף ותכ"ח והיית צריך לקצר אף רצועת התחומין לשיעור זה כדי שתהא מרובעת לשטת גדולי הרבנים. ולשטה אחרת שכתבנו שהיא עיקר אלו היית מודד מאמצע קרן העיר היית צריך לחסר פאה מטבלאות של קרנות לעשותה צורה זו# שאני מצייר לך עכשיו ואתה יודע שאתה צריך ליתן פאה לכל שובתי שבת ואם כן אתה צריך לעשות הטבלאות שבקרנות כל אחת מהן בפאה כגון זו#
תחום ערי לויה ר"ל תחום שבכל עיר ועיר של ארבעים ושמונה עיר לקלוט את הרוצח על הדרך שכבר ביארנו במקומו אלפים רוחב על פני היקף כל העיר וכשאתה מוציא מהם אלף רוחב על פני היקף כל העיר למגרש ר"ל להיותו פנוי שלא ליטע ושלא לזרוע אלא להניחו לנויי העיר נמצא חציים למגרש וחציין לשדות וכרמים ועל אותו חצי של מגרש נאמר במקרא מקיר העיר וחוצה אלף אמה סביב. ומה שנאמר כאן נמצא מגרש רביע כבר שאלו עליה בגמרא פלגא הוי. ותירצנה בשלשה פנים אחד על רביע של עיר ושל תחומין ושל קרנות ואחד על של תחומין ושל קרנות ואחד על הקרנות לבד מצד שנתבלבלו המפרשי' בתרף השמועה אני מפרשה על אחד מן הדרכים שהוזכרו בה כדי להקל על התלמידים והוא שתירצוה מתחלה שלא נאמ' מגרש רביע אלא בעיר שהיא אלפים על אלפים על מדת העיר השנויה בשמועה ושנמצאו תחומי העיר ארבע טבלאות של אלפים על אלפים וכן תחומי הקרנות ונמצאת כל טבלא מהם בתשברתה ארבע טבלאות של אלף על אלף שהרי כשתחלקנה בקו יוצא מצפונה לדרומה יהו שתי טבלאות של אלף רוחב באורך אלפים וכשתחלק כל אחד מאלו ממזרחה למערבה נמצאו ארבע של אלף ונמצא בין ארבעתם שש עשרה רצועות של אלף אמה רחב באלף אמה אורך וכן בארבע טבלאות של קרנות ונמצאות שלשים ושתים רצועות של אלף על אלף בהיקף העיר וכשאתה חולק הטבלאות בחציין להיות החצי הסמוך לעיר מגרש והחצי שחוצה לו לנטיעת שדות וכרמים אתה מוצא מארבע טבלאות של עיר למגרש ארבע רצועות של אלף רוחב באלפים אורך ונמצאו שמנה רצועות למגרש של אלף על אלף אבל מטבלאות הקרנות אין מתכונות למגרשי העיר אלא רביעית הטבלא שהיא רצוע' של אלף על אלף כגון הצורה הזאת# ונמצא למגרש שנים עשר רצועות של אלף על אלף משלשי' ושנים אלף והקש' וא"כ מה הועלת בפי' וי"ב מל"ב יותר משליש והוא אמר שהמגרש רביע ופירש שלא אמר שהוא רביע אלא בהצטרפו' גוף העיר שהיא אלפים על אלפים שנמצאת היא ארבע רצועות של אלף על אלף ונמצאו שלשים ושש רצועות ואמר שהמגרש הוא רביע הכל ר"ל של גוף העיר ושל טבלאות הקרנות. וחזר והקשה והרי עדיין לא שבנו מטעותנו שהרי י"ב מל"ו אינו אלא שליש דוקא. ותירץ כמה מרובע יתר וכו' כלומר שבעיר עגולה עסקינן הואיל והעיר עגולה אעפ"י שלענין תחומי שבת אתה מרבע היא ותחומיה וכן לענין מדידתה למתנת הלויים מכל מקום לענין מגרש אתה מניחה בעגולה ואמר שהמגרש רביע הכל אלו היה הכל מתרבע היו [ל"ו] אלף והיה המגרש י"ב אלף וכשתחזיר המגרשים לעולם ותחסר מהם הפיאות אתה מחסר מהם רבע כיתרון מרובע על העגול ונמצא המגרש ט' אלפי' בעגול [מל"ו] אלפים של תחום שבת וחזר אביי לפרשה בדרך זה בעצמו אלא שאינו חושב עמהם טבלאות של גוף העיר ופרשה בעיר שאין גופה אלף על אלף שנמצאו טבלאות של תחומיה ארבע רצועות של אלפים על אלף ונמצא בין כלם שמנה רצועות של אלף על אלף והקרנות י"ט טבלאות של אלף על אלף שהרי הקרנות אין משתנים לגודל העיר למיעוטה והרי הן כ"ד טבלאות של אלף על אלף וכשתסבב את המגרש ברבוע על הדרך שביארנו תחלה אתה נותן מגרש מתחומי העיר מכל הטבלאות חציין הסמוך לעיר והם ארבע רצועות של אלף על אלף ומתחומי הקרנות רביעיתן שהן ארבע רצועות גם כן של אלף על אלף ונמצאו שמנה רצועות של אלף על אלף למגרש. והוא שהקשה אם כן תלתא הוי ופרשה שהוא חוזר ומעגל רבועה על הדרך שהתבאר וחזרו השמנה לששה שהם רביע כ"ד. נמצא לפי' ראשון רביע של עיר ושל תחומין ושל קרנות ולאביי רביע של תחומין ושל קרנות. ומה שפי' רבינא אחר כן מאי רביע רביע דתחומין פירשו גאוני ספרד שלא חלק על אביי כלל אלא בירר את דבריו שאין בכלל רביע שלו גוף העיר כמו שפרשנו ולא דבר אלא על רביע של תחומין ר"ל של תחומין ושל קרנות שהכל בכלל תחומין הוא. ומכל מקום יש מפרשי' לרבינא שטה אחרת והוא שהחזירה לענין ראשון בעיר של אלפים על אלפים ואין גוף העיר בכלל וכשאמר שהמגרש רביע פירושו של תחומין והגירסא מאי רביע ותירץ דתחומין ופירושו מאי רביע כלומר באי זה מגרש אנו אומרין שהוא רביע ר"ל רביע כל ההיקף הן של תחומין הן של קרנות בגמרא דתחומין כלומר במגרש הבא מצד תחומין שהרי מגרש התחומין שמנה רצועות של אלף על אלף ושמנה מל"ב הוא רביע. ונמצא הענין שמגרש התחומין רביע של תחומין ושל קרנות. ומכל מקום יש גורסי' מאי רביע רביע דתחומין. ומפרשי' אותה בעיר שהיא אלף על אלף ובלא עגול שהמגרש רצועות של אלף על אלף והוא רביע תחומין שהתחומין מן הסתם הם ארבע רצועות של אלפים על אלפים שהם ששה עשר של אלף על אלף ונמצא מגרש עיר של אלף על אלף רביע מה שהוא תחום גמור מן הסתם שסתם עיר הוא של אלפים על אלפים ונמצאו תחומי הד' טבלאות של אלפים על אלפים. ולדעת רבינא מכל מקום לא היה מגרש אצל הקרנות אלא סביב העיר הואיל ולגבי מגרש לא נזכר בפסוק פאות ואעפ"י שלענין נתינתם ללוים כתיב פאות מכל מקום היו זורעין ונוטעים כנגד הקרנות ודי למגרש בארבע סביבות העיר.
ורב אשי פירשה במגרש הקרנות כלומר מגרש היה רביע של קרנות עצמם שהרי מגרש הקרן אינו אלא אלף על אלף וכלו ד' רצועות של אלף על אלף ולדעת ר' אשי לא היה מגרש כלל אלא בקרנות והוא שהקשו לו והא סביב כתיב שאעפ"י שרבינא מיעט של קרנות הרי מכל מקום יכול הוא לפרש סביב על רוחות העיר אבל אתה שאתה ממעט מגרש מסביבות העיר היאך אתה מפרש סביב ופי' סביב [דקרנות] מפני שהיה בכל קרן וקרן מארבע הרוחות כסביב האמור בעולה בארבעת הקרנות. ולרב אשי אתה יכול לפרשה בכל עיר שבעולם בין גדולה בין קטנה בין עגולה בין מרובעת. וכן אתה יכול לגרוס בו מאי רביע דקרנות או אם תרצה מאי רביע רביע דקרנות שהרי פירושו שמגרש הקרנות. הקרנות ומה שהקשו לרב אשי והא איכא מורשא דקרנאתא. לא על דברי רב אשי הקשו אלא תלמיד היה ושואלו ספקותיו והוא חוזר למה שאמר רב אדא למעלה שהמגרש נמדד בעגול ולא היה סבור מקשה זה שנהא אנו עסוקים בעיר עגולה אלא שהוא סבור שנפרשה בעיר מרובעת ואע"פ שהעיר מרבעת יהא המגרש נמדד בעגול ואחר שכן נמצאו קרנות העיר אוכלים תוך רביע הקרן המונח למגרש ואין כאן אלף מגרש והודיעו שבעיר עגולה הענין מתבאר. ואעפ"י שדרך כלל אנו אומרי' בעגולה שמרבעין אותה פירושו שרואי' אותה כמרובעת בין להלוך שבת להוסיף בתחומין בין לנתינת הלויים להוסיף בתחומין אבל לרבעה דוקא. ויש מפרשי' אותה על מה שחשב עם האמות גוף העיר שהוא אלפים על אלפים והא איכא מורשא דקרנאתא שהן ארבע מאות אמה לכל צד והיאך אי אתה מונה אלא ארבעת אלפים לבד וכן ראיתיה לגאוני ספרד ואין זה כלום שהרי מכל מקום אנו מונים בה ד' רצועות של אלף ואחר כך חזר ושאלו על שמועה ראשונה האמורה לענין תחומי שבת שהעיר שהיא אלפים על אלפים משתכר ברבוע תחומיה ת"ת אמה והלא אין המרובע יתר על העגול אלא רביע [מלבר] שהוא שליש מלגאו ושלישו של אלפים אינו אלא שש מאות וששים ושבע פחות שליש אמה. ותירץ הני מילי ברבועא אבל בהלוכא בעינן טפי כלומר כל שיש כאן עגול שהוא ארבע אמות ברחבו מצד לצד שהיקפו שתים עשרה אמה כמו שידוע בכלל כל שיש ברחבו טפח יש בהיקפו שלשה טפחי' כשאתה מרבעו מלבר ומוסיף עליו קרנות אתה צריך בהיקפו לחוט שש עשרה נמצא שבדרך היקף המרובע יתר על העגול רביע מלבר שהוא שליש מלגו אבל כשאינך בא מדרך היקף סבובי אלא בחוט בקו ישר כל שאם אתה נותן את החוט מצפון לדרום של מרובע זה או שמערבו למזרחו אתה נותן ד' אמות כשאתה נותנו באלכסון אתה צריך בו לחוט גדול מחברו יותר מרביע וכל שיש ברחבו ארבע אמות יש מקרן לקרן באלכסונו חמש אמות ושלשה חומשי אמה. שהאלכסון מוסיף שני חומשין לכל אמה לחשבון כל אמתא ברבועא אמתא ותרין חומשי באלכסונא:
קישורים חיצוניים
צורת הדף: באתר היברובוקס • באתר דף יומי (עם אפשרות האזנה) • באתר שיתופתא
הדף עם פרשנים: באתר "תא שמע" • באתר "על התורה" • באתר "ספריא" • באתר "מרכז שטיינזלץ" • ביאור "חברותא" באתר ויקישיבה